
Calculating E from V(x,y,z) E = potential gradient Electrostatic
Relation between field & potential Calculating E from V (x,y,z): E = - potential gradient Google Classroom About Transcript Let's calculate the electric field vector by calculating the negative potential gradient. We first calculate individually calculate the x,y,z component of the field by partially differentiating the potential function.

Electric field as potential gradient 12th physics SWAJ Foundation
An electric field gradient is a measure of how the electric field changes with respect to position within a region of space. It is a vector quantity that describes the rate of change of the electric field in each direction.
Electric Potential Electric Field as Potential Gradient
In atomic, molecular, and solid-state physics, the electric field gradient ( EFG) measures the rate of change of the electric field at an atomic nucleus generated by the electronic charge distribution and the other nuclei.

(a) Electric field gradient distribution (V/m), (b) 3D top view of the
In vector calculus notation, the electric field is given by the negative of the gradient of the electric potential, E = − grad V. This expression specifies how the electric field is calculated at a given point. Since the field is a vector, it has both a direction and magnitude.

Electric Field as Potential Gradient FSc Class 12 PHYSICS Chapter
As shown in Figure 7.5.1, if we treat the distance Δs as very small so that the electric field is essentially constant over it, we find that. Es = − dV ds. Therefore, the electric field components in the Cartesian directions are given by. Ex = − ∂V ∂x, Ey = − ∂V ∂y, Ez = − ∂V ∂z. This allows us to define the "grad" or.

Simulation of electric field gradient squared for cylindrical IDE
A numerical model of oil-solid multi-gradient filtration with electric field enhancement was developed by coupling the electric field governing equation, flow field governing equations, discrete phase tracking equation, and particle-wall collision model equation.. When the electric field strength is 2 kV/mm, the inlet flow rate is 0.3 m.

Lecture 4 Review of electrostatics pt. 2
The gradient of the electric field is the second derivative of the electrostatic potential, and as such, it obeys certain symmetries; The EFG is a symmetric tensor with zero trace.
a) Electric field gradient distribution at the tip region under DC bias
7.14. With this notation, we can calculate the electric field from the potential with. E→ = −∇ V, E → = − ∇ → V, 7.15. a process we call calculating the gradient of the potential. If we have a system with either cylindrical or spherical symmetry, we only need to use the del operator in the appropriate coordinates: Cylindrical:∇.

Electric field intensity as negative potential gradient YouTube
5.14: Electric Field as the Gradient of Potential. where E(r) E ( r) is the electric field intensity at each point r r along C C. In Section 5.12, we defined the scalar electric potential field V(r) V ( r) as the electric potential difference at r r relative to a datum at infinity. In this section, we address the "inverse problem.

Are All Electric Field The Gradient Of A Potential Dr Bakst
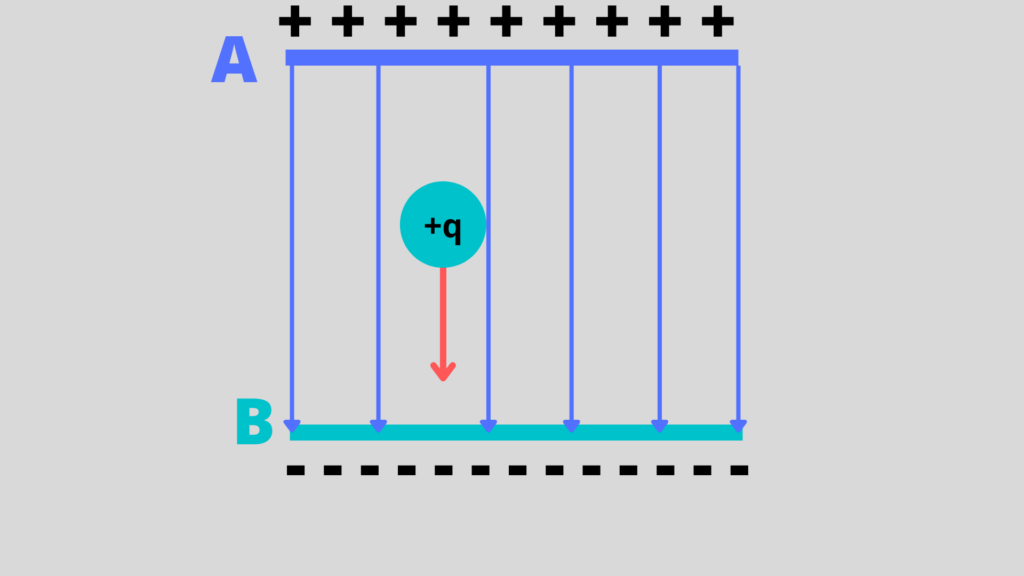
See the text for details.) The work done by the electric field in Figure 19.2.1 19.2. 1 to move a positive charge q q from A, the positive plate, higher potential, to B, the negative plate, lower potential, is. W = −ΔPE = −qΔV (19.2.1) (19.2.1) W = − Δ P E = − q Δ V. The potential difference between points A and B is.

Finite element simulation with COMSOL; areas with different color
Electric Field as the Gradient of Potential In Section 5.8, it was determined that the electrical potential difference measured over a path is given by (5.14.1) where is the electric field intensity at each point along . In Section 5.12, we defined the scalar electric potential field as the electric potential difference at

Electric Field as potential gradient Class 12 ElectrostaticsNCERT
The gradient of a scalar field is a vector that points in the direction in which the field is most rapidly increasing, with the scalar part equal to the rate of change. A particularly important application of the gradient is that it relates the electric field intensity \({\bf E}({\bf r})\) to the electric potential field \(V({\bf r})\).

Relation Between Potential Gradient And Electric Field YouTube
The electric field is the gradient of the potential. The gradient is in the direction of the most rapid change of the potential, and is therefore perpendicular to an equipotential surface. If $\FLPE$ were not perpendicular to the surface, it would have a component in the surface. The potential would be changing in the surface, but then it.

Contour plot of gradient of squared electric field strength, ∇E 2 rms
Electric fields are caused by electric charges, described by Gauss's law, and time varying magnetic fields, described by Faraday's law of induction. Together, these laws are enough to define the behavior of the electric field. However. is the gradient of the electric potential and.

Activating function (AF, gradient of the electric field) of the
Electric Field as Gradient. The expression of electric field in terms of voltage can be expressed in the vector form . This collection of partial derivatives is called the gradient, and is represented by the symbol ∇ .The electric field can then be written. Expressions of the gradient in other coordinate systems are often convenient for taking advantage of the symmetry of a given physical.
PPT Measuring Polarizability with an Atom Interferometer PowerPoint
Droplet directional transport is one of the central topics in microfluidics and lab-on-a-chip applications. Selective transport of diverse droplets, particularly in another liquid phase environment with controlled directions, is still challenging. In this work, we propose an electric-field gradient-driven droplet directional transport platform facilitated by a robust lubricant surface. On the.